
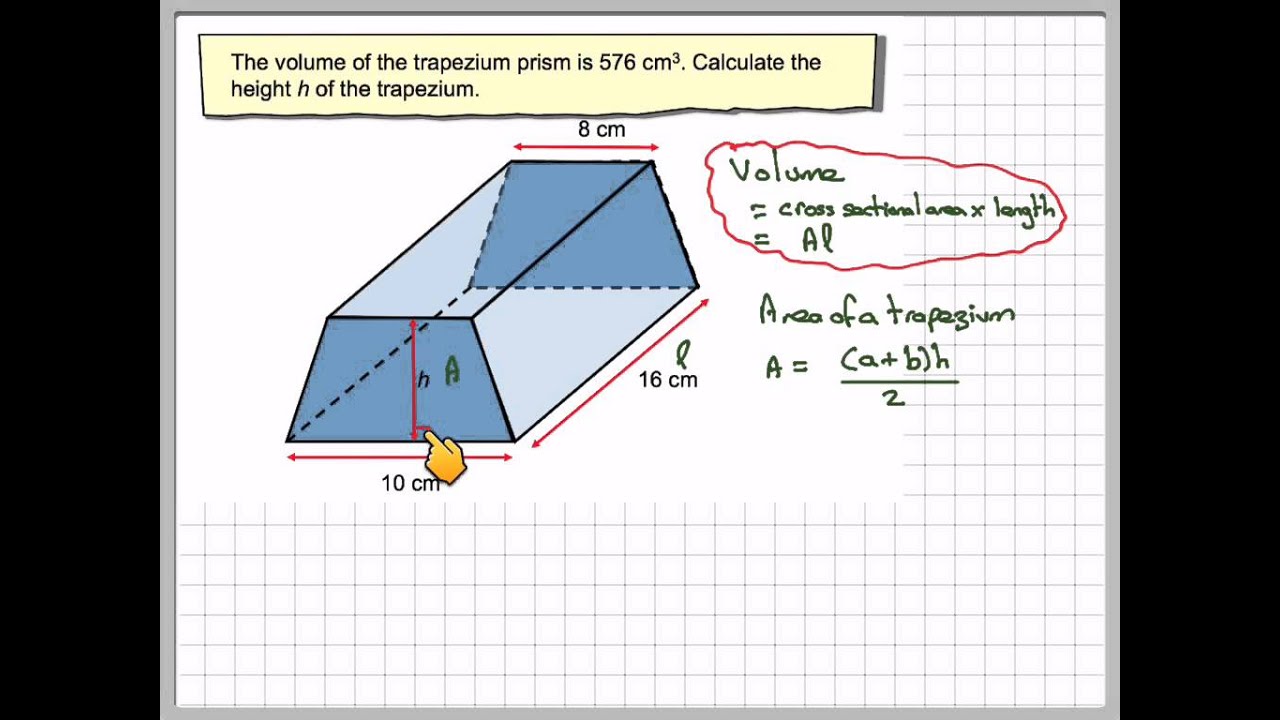
The surface area is the sum of the areas of all the sides of an 3D object, incising its base and top.įor the surface area calculation, we will use the same trapezoidal prism as the last example.
#Trapezoidal prism how to#
Hence, the lateral area of this trapezoidal prism is 10 m × (4 m + 7 m + 4 m + 3 m) = 180 m².Īfter understanding how to find the lateral area of a trapezoidal prism, let's talk about surface area. The last step is to compute the lateral area using the following formula: For this trapezoidal prism, these lengths are 4 m, 7 m, 4 m, and 3 m respectively.Ĭompute the volume of the trapezoidal prism You can see sides a, b, c and d in the diagram. In this example, the length of the trapezoidal prism is 10 m.įor our example, the height of the trapezoidal prism is 7 m.ĭetermine the lengths of sides a, b, c, and d You can calculate the lateral area of a trapezoidal prism in four steps: To understand the calculation of the lateral area of a trapezoidal prism, let's take the following trapezoidal prism as an example: Check out our rectangular prism calculator for more information. I'm not sure whether you are expected to know this though.The lateral area is the sum of the areas of all the sides of an 3D object besides the base and the top. In general the formula to compute such a shape with height $h$, top rectangle $a\times b$ and bottom rectangle $c \times d$, with the $a$ side parallel to the $c$ side, is $\frac16 h(2ab+2cd+ad+bc)$. Assuming the faces are still plane, the cross-section at height $x$ (measured in $m$) is given by $(10-x)\times(8-\frac 32 x)$, and the volume can be determined by integration to yield $V = \int_0^2(10-x)(8-\frac 32 x)dx = 118 m^3$. If the top and bottom faces of the stack are laid out as hinted in the question, with the bottom $10m$ parallel to the top $8m$ and the bottom $8m$ parallel to the top $5m$, it is neither a trapezium prism nor a truncated pyramid, because the non-horizontal edges do not intersect in a single point. In case the $8m$ on top and bottom are parallel, you have a trapezium prism, with trapezium area $(10m+5m)/2 \times 2m$ and "height" $8m$ (perpendicular to the trapezium), resulting in a volume of $120 m^3$.
Furthermore the question might be ambiguous whether the $8m$ edge of the top face is parallel or perpendicular to the $8m$ edge of the bottom face, and this affects the final result. The pyramid-based answers do not work because the trapezoidal prism is not actually part of a pyramid: the non-horizontal edges do not meet in a single point. Identify the parallel sides of the base (trapezoid) to be $b_ I am confused what is the correct approach. I saw online different methods giving different answers to this question. I also assume a prism is the same thing as a pyramid for geometrical purposes.Ī trapezoidal prism is a 3D figure made up of two trapezoids that is joined by four rectangles. I only confusion I have about this problem is the calculation of the volume of the stack which I believe is the trapezoidal prism (or truncated (right) rectangular prism or frustum of (right) rectangular prism). I know the approach needed to solve this problem. By how many centimetres can the level be raised?

For a plot of land of 100 m × 80 m, the level is to be raised by spreading the earth from a stack of a rectangular base 10 m × 8 m with vertical section being a trapezium of height 2 m.


 0 kommentar(er)
0 kommentar(er)
